Econ 265: Introduction to Econometrics

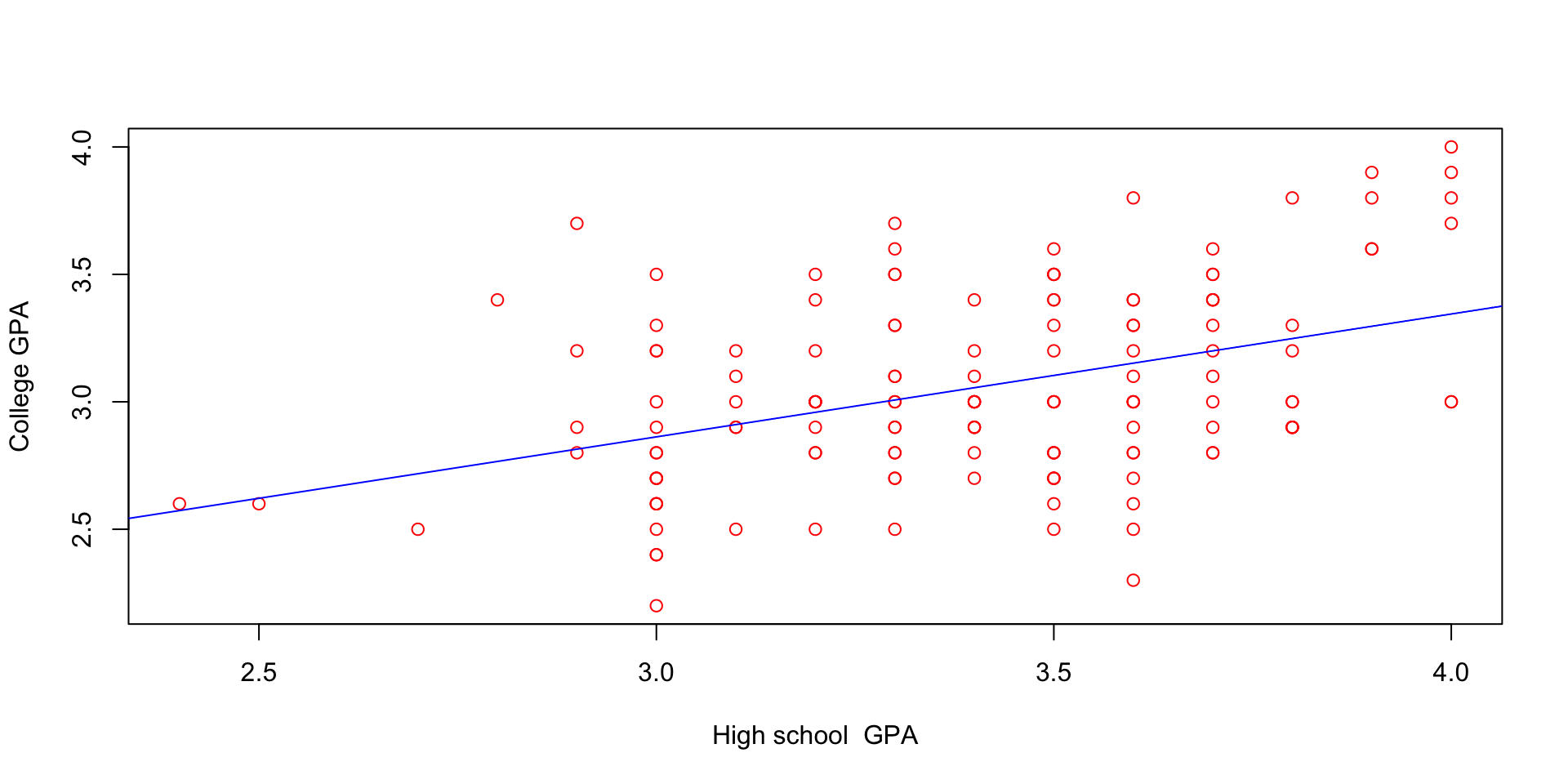
Topic 3: Simple Linear Regression

Moshi Alam

Introduction

• With regressions we want to make statistical associations between \(y\) and \(x\)’s in the population using sample
• You have learnt the fundamentals in Econ 160
• Here in addition, we will be
  • more formal
  • apply in code
• Readings: Ch-2 of Wooldridge and these slides

Foundations of Regression Analysis

Population vs. Sample

Simple linear regression model (SLRM): studies how \(y\) changes with changes in \(x\)

Population Model: \[y_i = β₀ + β₁x_i + u_i\]

• β₀: Population intercept parameter
• β₁: Population slope parameter
• \(u_i\): Error term (unobserved factors)
• Example: \(wages_i = β₀ + β₁education_i + u_i\)

Estimation from a sample gives: \[\hat{y_i} = \widehat{\beta_0} + \widehat{\beta_1} x_i\]

• \(\widehat{\beta_0}\): estimated intercept
• \(\widehat{\beta_1}\): estimated slope
• \(\hat{u_i}\): Residuals = \(\hat{y_i} - y_i\)

Note

• parameters by defintion are model-defined population constants (not random variables)
• “hats” refer to estimates
• If I write \(y\) instead of \(y_i\) that means I am referring to the entire vector of all \(y_i\)’s

Population Model: \[y_i = β₀ + β₁x_i + u_i\]

• If the other unobserved factors in u are held fixed,
  • so that the changes in u is zero,
• then x has a linear effect on y
• simply: \(\Delta y_i = \beta_1 \Delta x_i\) iff \(\Delta u_i = 0\)
• Formally, \(\frac{\partial y_i}{\partial x_i} = \beta_1\) iff \(\frac{\partial u_i}{\partial x_i} = 0\)

Note

• We are imposing an assumption on the relation between \(x\) and \(u\) to be able to interpret \(\beta_1\).
• Lets formalize.

Assumptions

Key Assumptions About \(u\)

• Assumptions
• Why is \(E(u)=0\) just a normalization?

1. Zero Mean: \(E(u) = 0\)

• Simple normalization of unobservables
• Can always redefine intercept to make this true

Why This Works

• Requires intercept in the regression
• Redefining intercept absorbs any non-zero mean

2. Mean Independence: \(E(u|x) = E(u)\)

• Average error same for all values of \(x\)
• Stronger than zero correlation
• Very strong assumption

Implications

• Combines with first assumption to give:
• \(E(u|x) = 0\) (Zero Conditional Mean)
• Essential for interpreting \(\beta_1\) as causal effect

Original Model

\(wage_i = \beta_0 + \beta_1educ_i + u_i\)

Where \(u\) includes ability:

• Average ability = 100 (IQ points)
• So \(E(u) = 100 \neq 0\)

Rewritten Model

\(wage_i = (\beta_0 + 100) + \beta_1educ_i + \tilde{u_i}\)

Where:

• \(\tilde{u} = u - 100\) is deviation from mean
• Now \(E(\tilde{u}) = 0\)
• New intercept = \(\beta_0 + 100\)
• Same model, different parameterization

What about \(E(u \mid x) = 0\)?

• Let us go back to the wage and education example

\[ wage_i = \beta_0 + \beta_1 education_i + u_i \]

• what does mean independence and thereby zero conditional mean, mean here?
• is it too strong an assumption?

Population Regression Function

• Population Regression Function
• Sample Visualization
• Components of y

Zero conditional mean implies:

\(E(y_i|x_i) = \beta_0 + \beta_1x_i\)

Interpretation

• Linear function of x
• 1 unit \(\uparrow\) in x changes \(E(y)\) by \(\beta_1\)
• Given x, distribution of y centered around \(E(y|x)\)

gpa1 data

\(E(colGPA|hsGPA) = 1.5 + 0.5 \, hsGPA\)

For \(hsGPA = 3.6\):

• Average \(colGPA = 1.5 + 0.5(3.6) = 3.3\)
• Not every student gets 3.3
• Some higher, some lower
• Depends on unobserved factors (u)

library(wooldridge)
# gpa_model <- lm(colGPA ~ hsGPA, data = gpa1)
# summary(gpa_model)
plot(gpa1$hsGPA, gpa1$colGPA,
     xlab = "High school  GPA",
     ylab = "College GPA",
     col = "red")
abline(lm(gpa1$colGPA ~ gpa1$hsGPA), col = "blue")

Systematic Part

• \(\beta_0 + \beta_1x = E(y|x)\)
• Explained by \(x\)
• Population regression line
• Blue line shows \(E(y|x)\) assuming linear model

Unsystematic Part

• \(u\) = Deviation from \(E(y|x)\)
• Not explained by \(x\)
• Zero mean at each \(x\): \(E(u \mid x) = 0\)

set.seed(123)
n <- 1e5
u1 <- rnorm(n, mean=0.0, sd=0.1)
x <- sin(seq(-5, 5, length.out=n))
u2 <- x + rnorm(n, mean=0, sd=0.1)
cat("Mean of u1:", mean(u1), "\n", "Mean of u2:", mean(u2), "\n")

Mean of u1: 9.767488e-05 
 Mean of u2: 0.0005215476 

par(mfrow=c(1,2))
p1 <- plot(x, u1, main="E(u)=0 and E(u|x)=0")
abline(lm(u1~x), col="red", lwd=2)
p2 <- plot(u2, x, main="E(u)=0 but E(u|x)!=0")
abline(lm(u2~x), col="red", lwd=2)

Deriving the OLS estimator

Starting assumption to deriving OLS estimators

We start with two key assumptions:

1. \(E(u) = 0\)
2. \(E(u \mid x) = 0\) (zero conditional mean)

Using this we can show that:

• \(Cov(x,u) = E(xu) - E(x)E(u)\)
• Since \(E(u) = 0\):
  • \(Cov(x,u) = E(xu) - E(x) \cdot 0 = E(xu)\)
• Therefore: \(Cov(x,u) = 0 \iff E(xu) = 0\)

Derivation

Population Model: \[y_i = β₀ + β₁x_i + u_i\]

• Assumptions on the population:
  • \(E(u) = 0\)
  • Covariance between \(x\) and \(u\) is zero: \(\text{Cov}(x,u) = 0\)
    • These imply: \(E(xu) = 0\)
• Implications:
  • In terms of observable variables \(x\) and \(y\):
    • \(E(y - \beta_0 - \beta_1x) = 0\)
    • \(E[x(y - \beta_0 - \beta_1x)] = 0\)
  • Assumptions give us these moment conditions

Sample counterparts

• Given a sample of data
• estimates \(\hat{\beta_0}\) and \(\hat{\beta_1}\) solve the sample counterparts of the moment conditions,
  • leading to equations:

\[\frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0\]

\[\frac{1}{n} \sum_{i=1}^{n}x_i(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0\]

• These equations can be solved for \(\hat{\beta_0}\) and \(\hat{\beta_1}\).

Now, \(\frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0\), simplifies to

\[\bar{y_i} = \hat{\beta_0} + \hat{\beta_1}\bar{x_i}\]

Where \(\bar{y_i} = \frac{1}{n} \sum_{i=1}^{n}y_i\) is the sample average of the \(y_i\).

Thus,

\[\hat{\beta_0} = \bar{y_i} - \hat{\beta_1}\bar{x_i}\]

Plug in \(\hat{\beta_0}\) into: \(\frac{1}{n} \sum_{i=1}^{n}x_i(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0\) and simplifying gives us the slope coefficient \(\hat{\beta_1}\):

\[\hat{\beta_1} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})^2}\]

provided, \(\sum_{i=1}^{n}(x_i - \bar{x})^2 > 0\). What’s this?

Note that \(\hat{\beta_1} = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})^2}\) is nothing but

the sample covariance divided by the sample variance,

which can be written as,

\[\hat{\beta}_1=\hat{\rho}_{x y} \cdot\left(\frac{\hat{\sigma_y}}{\hat{\sigma_x}}\right)\]

since,

• sample covariance \(= \hat{\rho}_{x y} \cdot \hat{\sigma_y}\hat{\sigma_x}\)
• correlation coeff: \(\hat{\rho}_{x y}\)
• sample variance \(= \hat{\sigma_x}^2\)

Interestingly

• the line (characterized by an intercept and a slope) that minimizes: \[\sum_{i=1}^n \hat{u}_i^2= \underbrace{\sum_{i=1}^n\left(y_i-\hat{\beta}_0-\hat{\beta}_1 x_i\right)^2}_{\text{SSR: Squared Sum of Residuals}}\]

• lead to FOC’s that are same as what we obtained as the sample counterparts of the moment conditions

  • \(\frac{1}{n} \sum_{i=1}^{n}(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0\)
  • \(\frac{1}{n} \sum_{i=1}^{n}x_i(y_i - \hat{\beta_0} - \hat{\beta_1}x_i) = 0\)

• that we used to derive the OLS estimates

• OLS chooses \(\hat{\beta_0}\) and \(\hat{\beta_1}\) to minimize SSR

• Let us implement in R and test with the lm package

Quick recap

• Main assumptions on the population: \(E(u) = 0\) and \(E(u \mid x) = 0\)
• Gives us moment conditions which we can convert to sample counterparts invoking LLN
• Solving the sample counterparts gives us the OLS estimates

Statistical properties of OLS

Fitted values and residual

• The estimates of \(\beta_0\) and \(\beta_1\) thus obtained are called OLS
• Can obtain “fitted values” of \(y_i\): \[\hat{y_i} = \hat{\beta_0} + \hat{\beta_1} x_i\]
• Obtain residuals: \(\hat{u_i} = y_i - \hat{y_i} = y_i - \hat{\beta_0} - \hat{\beta_1} x_i\)

Properties

• Sample mean of residuals is zero \(\frac{1}{n} \sum_{i=1}^{n} \hat{u}_i = 0\)
• Sample mean of x and y \((\bar{x}, \bar{y})\) lies on the regression line
• The sample covariance between the regressors (\(x\)) and the OLS residuals is zero \(\frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})\hat{u}_i = 0\)
• Predictions and residuals are uncorrelated \(\frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - \bar{y})\hat{u}_i = 0\)

Try testing these out with this generated data:

set.seed(123)
x <- seq(1, 100, length.out = 50)
y <- 2 + 3*x + rnorm(50, 0, 20) #DGP
plot(x, y, main="Linear Relationship Example")
abline(lm(y ~ x), col="red", lwd=2)

Decomposition

• Total Sum of Squares (SST): \[ \text{SST} \equiv \sum_{i=1}^{n}(y_i - \bar{y})^2 \]

• Explained Sum of Squares (SSE): \[ \text{SSE} \equiv \sum_{i=1}^{n}(\hat{y}_i - \bar{y})^2 \]

• Residual Sum of Squares (SSR): \[ \text{SSR} \equiv \sum_{i=1}^{n}\hat{u}_i^2 \]

Relationship Between Sums of Squares

Total variation in \(y\) can be expressed as:

\[ \text{SST} = \text{SSE} + \text{SSR} \]

Proof Outline To prove this relationship, we can write:

\[ \sum_{i=1}^{n}(y_i - \bar{y})^2 = \sum_{i=1}^{n}[(\hat{y}_i - \bar{y}) + (y_i - \hat{y}_i)]^2 \] \[ = \sum_{i=1}^{n}(\hat{u}_i + (y_i - \bar{y}))^2 \] \[ = \text{SSR} + 2\sum_{i=1}^{n}\hat{u}_i(y_i - \bar{y}) + \text{SSE} \]

R-squared

• Measures goodness of fit \[R^2 = \frac{SSE}{SST} = 1 - \frac{SSR}{SST}\]
• Ranges from 0 to 1
• Interpretation: Proportion of variance explained by model

# Calculate R-squared
summary(model)$r.squared

[1] 0.6510794

# Decomposition of variance
anova(model)

Analysis of Variance Table

Response: dist
          Df Sum Sq Mean Sq F value   Pr(>F)    
speed      1  21186 21185.5  89.567 1.49e-12 ***
Residuals 48  11354   236.5                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Expected Values and Variances of the OLS Estimator

Overview

• For any estimator we want to know two important things
  • Whether we are getting unbiased estimates
  • If yes, how precisely can we obtain those estimates
• Will require assumptions
• For OLS, we have 5 of them, which will constitute the Gauss-Markov assumptions

Expected Value of the OLS Estimator

Unbiasedness of an estimator

An estimator is unbiased if, on average, it produces estimates that are equal to the true value of the parameter being estimated.

Definition

An estimator producing an estimate \(\hat{\theta}\) for a parameter \(\theta\) is considered unbiased if: \[ \mathbb{E}(\widehat{\theta}) = \theta \]

Basically means that the sampling distribution of \(\hat{\theta}\) is centered around the true \(\theta\) on average

We will now show that the OLS estimator for a SLR model’s parameters \((\beta_0, \beta_1)\) is unbiased

Assumptions to prove unbiasedness of OLS

• SLR 1 - 4
• SLR1
• SLR2
• SLR3
• SLR4

1. Linear in parameters
2. Random sampling
3. Sample Variation in X
4. Zero Conditional mean

1. Linear in parameters:

   In the population model, the dependent variable, \(y\), is related to the independent variable, \(x\), and the error (or disturbance), \(u\), as: \[ y=\beta_0+\beta_1 x+u \] where \(\beta_0\) and \(\beta_1\) are the population intercept and slope parameters, respectively.

2. Random Sampling

   We have a random sample of size n,\(\left\{\left(x_i, y_i\right): i=1,2, \ldots, n\right\}\) in the population model

3. Sample variation in X

   The sample explanatory x variable, namely, \(x_i\) , \(i \in \{1, \cdots, n\}\) , are not all the same value \[\widehat{Var}(x_i) > 0\]

4. Zero conditional mean

The error \(u\) has an expected value of zero given any value of the explanatory variable. In other words, \[E(u \mid x)=0\] .

Theorem

Theorem: Unbiasedness of the OLS estimator

Using Assumptions SLR. 1 through SLR.4,

\[ \mathrm{E}\left(\hat{\beta}_0\right)=\beta_0 \text { and } \mathrm{E}\left(\hat{\beta}_1\right)=\beta_1 \]

• In other words, \(\hat{\beta}_0\) is unbiased for \(\beta_0\), and \(\hat{\beta}_1\) is unbiased for \(\beta_1\).
• Let us prove it using our assumptions!
• In doing so, we will learn some tricks, and I want you to learn the tricks and observe the patterns in the art of going about an econoemtric proof.

Key patterns in the proof

• Start with the OLS estimate \(\hat{\beta}_1 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})^2}\) and \(\hat{\beta}_0 = \bar{y} - \hat{\beta}_1\bar{x}\)
• Write the OLS estimator in terms of the population parameters
  • To do this we have to bring in \(y_i\) (population model) and not \(\hat{y_i}\)
    • This is what brings in the population parameters \(\beta_0\) and \(\beta_1\) on the RHS
  • Tricks to bring in \(y_i\) in the OLS estimator:
    • Without any assumptions we showed and used:
    • \(\sum_{i=1}^n(x_i - \bar{x})(y_i - \bar{y}) = \sum_{i=1}^n(x_i - \bar{x})y_i\)
      • Could have written this as \(\sum_{i=1}^n(y_i - \bar{y})x_i\) but did not to bring in \(y_i\)
  • Other tricks: Without any assumptions
    • \(\sum_{i=1}^n(x_i - \bar{x}) = 0\)
    • \(\sum_{i=1}^n(x_i - \bar{x})x_i = \sum_{i=1}^n(x_i - \bar{x})^2\)
• Take the expectation conditional on \(x_i\)
  • impose the SLR assumptions on zero mean and zero conditional mean
  • use LIE

Variance of the OLS Estimators

Sampling distribution of the OLS estimators

• population model: \(y_i = \beta_0 + \beta_1 x_i + u_i\)
• The OLS estimates \(\hat{\beta}_0\) and \(\hat{\beta}_1\) are random variables because they depend on the random sample \(\left\{\left(x_i, y_i\right): i=1,2, \ldots, n\right\}\)

SLR 5: Homoskedasticity assumption

The population error \(u_i\) has the same variance given any value of \(x_i\), i.e.,

\[ Var(u \mid x) = \sigma^2 \]

SLR 5 further implies that \(\sigma^2\) is also the unconditional variance of \(u\).

\[\operatorname{Var}(u \mid x)=\mathrm{E}\left(u^2 \mid x\right)-[\mathrm{E}(u \mid x)]^2\]

\[ \text { and since } \mathrm{E}(u \mid x)=0, \sigma^2=\mathrm{E}\left(u^2 \mid x\right)\]

Now we have \(Var( y \mid x)\)

using Assumptions SLR. 4 and SLR. 5 we can derive the conditional variance of \(y\) :

\[ \begin{gathered} \mathrm{E}(y \mid x)=\beta_0+\beta_1 x \\ \operatorname{Var}(y \mid x)=\sigma^2 \end{gathered} \]

From here we can get \(Var(u \mid x)\)

Homoskedasticity

Theorem

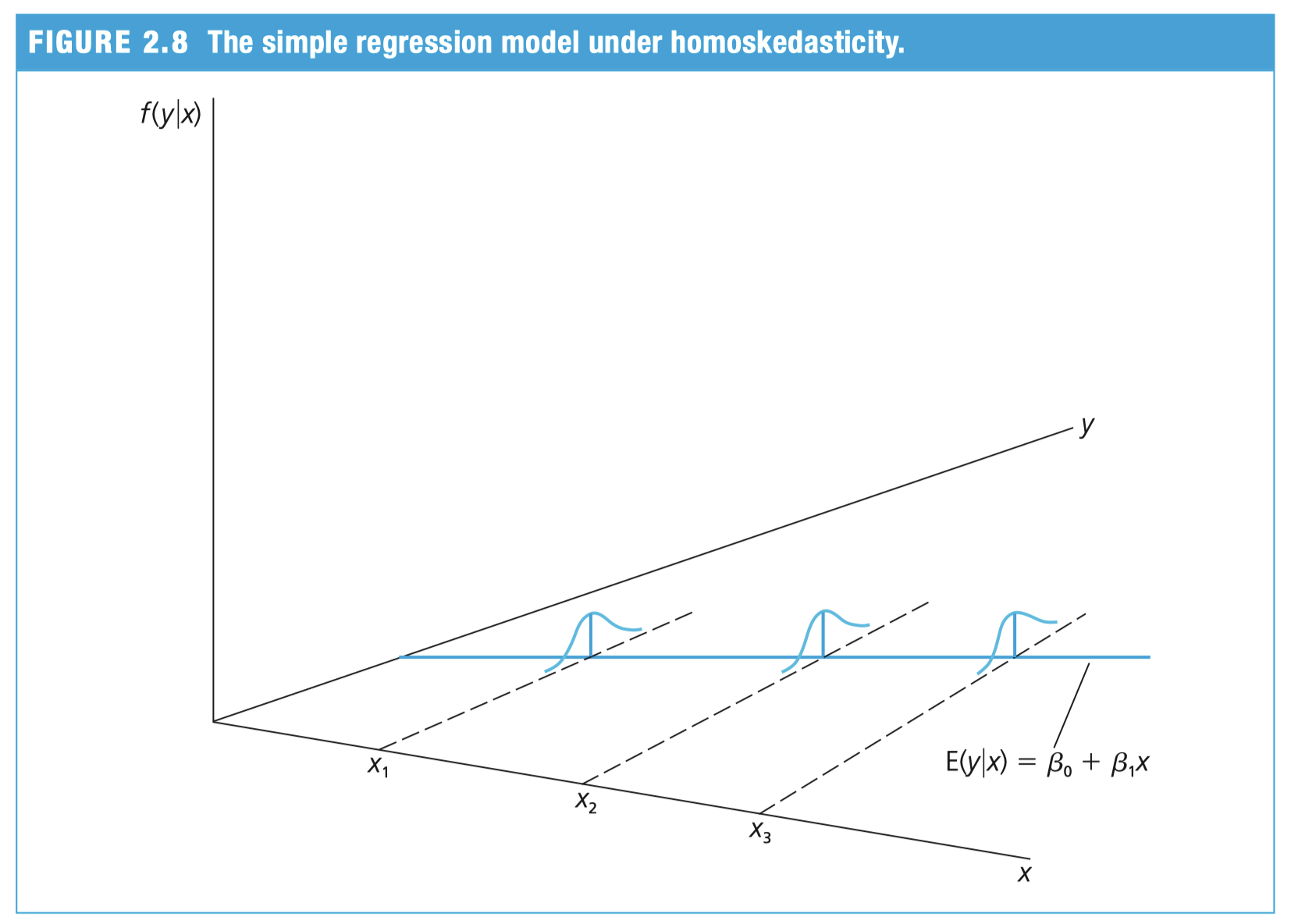
Sampling variance of OLS estimators

Under Assumptions SLR. 1 through SLR.5,

\[ \operatorname{Var}\left(\hat{\beta}_1\right)=\frac{\sigma^2}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} = \frac{\sigma^2}{\mathrm{SST}_x}, \]

and

\[ \operatorname{Var}\left(\hat{\beta}_0\right)=\frac{\sigma^2 \frac{1}{n} \sum_{i=1}^n x_i^2}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} = \frac{\sigma^2 \frac{1}{n} \sum_{i=1}^n x_i^2}{\mathrm{SST}_x} \]

where these are conditional on the sample values \(\left\{x_1, \ldots, x_n\right\}\).

• Let us prove this!

Proof of \(\operatorname{Var}\left(\hat{\beta}_1\right)\)

• Let us work with \(\hat{\beta}_1 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})^2}\) \(\implies\) \(\hat{\beta}_1 = \beta_1 + \frac{\sum_{i=1}^{n}(x_i - \bar{x})u_i}{\sum_{i=1}^{n}(x_i - \bar{x})^2}\)
• Denote \((x_i - \bar{x})\) as \(d_i\). So \(\hat{\beta}_1 = \beta_1 + \frac{\sum_{i=1}^{n} d_iu_i}{\sum_{i=1}^{n}(x_i - \bar{x})^2}\)
• Now take the variance of \(\hat{\beta}_1\) conditional on the sample values \(x_i\)

\[\begin{align*} \operatorname{Var}\left(\hat{\beta}_1\right) & = \operatorname{Var}\left(\beta_1 + \frac{\sum_{i=1}^{n} d_iu_i}{SST_x}\right) \\ & = \operatorname{Var}\left(\frac{\sum_{i=1}^{n} d_iu_i}{SST_x}\right) \quad \text{skipping 2 steps} \\ & = \frac{1}{\left(SST_x\right)^2} \sum_{i=1}^{n} d_i^2 \operatorname{Var}(u_i) \quad \text{skipping 3 steps} \\ & = \frac{\sigma^2}{SST_x} \end{align*}\]

Measure of precision of \(\hat{\beta_1}\)

• \(sd(\hat{\beta}_1) = \sqrt{\operatorname{Var}\left(\hat{\beta}_1\right)}\) gives a measure of the precision of \(\hat{\beta}_1\)
• But we do not know \(\sigma^2\) so we do not know \(sd(\hat{\beta}_1)\)
• So we have to estimate \(\sigma^2\) to get an estimate of \(sd(\hat{\beta}_1)\)
• The estimate of the \(sd(\hat{\beta}_1)\) is called the standard error of \(\hat{\beta}_1\)

Theorem

Unbiased estimation of \(\sigma^2\)

Under Assumptions SLR. through SLR.5,

\[\mathrm{E}\left(\hat{\sigma}^2\right)=\sigma^2\]

where \(\hat{\sigma}^2=\frac{1}{n-2} \sum_{i=1}^n \hat{u}_i^2\), where \(\hat{u}_i=y_i-\hat{\beta}_0-\hat{\beta}_1 x_i\)

• Study the proof from 2-5c
• Try to observe the patterns in the proof similar to the unbiasedness proof of the OLS estimates

In essence we have shown

Assuming SLR 1-5, and conditional on the sample values \(\left\{x_1, \ldots, x_n\right\}\), we have shown that:

• The OLS estimators are unbiased
  • \(\mathrm{E}\left(\hat{\beta}_0\right)=\beta_0\) and \(\mathrm{E}\left(\hat{\beta}_1\right)=\beta_1\)
• We can obtain the variance of the OLS estimators
  • \(\operatorname{Var}\left(\hat{\beta}_1\right)=\frac{\sigma^2}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} = \frac{\sigma^2}{\mathrm{SST}_x}\)
  • \(\operatorname{Var}\left(\hat{\beta}_0\right)=\frac{\sigma^2 \frac{1}{n} \sum_{i=1}^n x_i^2}{\mathrm{SST}_x}\)
• But we do not know \(\sigma^2\)
  • The residual variance \(\hat{\sigma}^2\) is unbiased for the variance of the population errror \(\sigma^2\)
  • \(\mathrm{E}\left(\hat{\sigma}^2\right)=\sigma^2\)
• And we learnt a lot of tricks and pattern recognition in the process
• And some stuff about how to work with data

Heteroskedasticity in SLR

• Heteroskedasticity: \[Var(u_i \mid x_i)=\sigma^2(x_i) \quad \text{(not constant)}\]
• Under SLR1–SLR4 (but not SLR5):
  • OLS remains unbiased for \((\beta_0,\beta_1)\)
  • Usual variance formulae and standard errors are invalid
  • OLS is no longer efficient among linear unbiased estimators
• Large-sample variance (idea): weights depend on \(u_i^2\)
• Fix (inference): use heteroskedasticity-robust (White/Eicker–Huber) SEs
  • Same point estimates, different (robust) standard errors

Warning

Heteroskedasticity is common in cross-sectional data (wages, firm sizes, housing prices)

library(lmtest)  # for BP test
library(sandwich)  # for robust SEs

# Generate data with heteroskedasticity
set.seed(456)
n <- 1000
educ <- rnorm(n, 12, 3)
exper <- runif(n, 0, 20)
u <- rnorm(n, 0, sd = 0.5 + 3*educ^2)
wage <- 10 + 2*educ + u

model <- lm(wage ~ educ)

# Breusch-Pagan test for heteroskedasticity
bptest(model)

    studentized Breusch-Pagan test

data:  model
BP = 184.4, df = 1, p-value < 2.2e-16

plot(fitted(model), residuals(model), 
     main="Residuals vs Fitted", xlab="Fitted values", 
     ylab="Residuals", pch=20, col="darkblue")
abline(h=0, col="red", lty=2)

Recommendation to get robust SEs

In the lm function, use:

library(sandwich)
library(lmtest)

model <- lm(wage ~ educ)
coeftest(model, vcov = vcovHC(model, type = "HC1"))

t test of coefficients:

            Estimate Std. Error t value Pr(>|t|)
(Intercept)   9.4847    76.1247  0.1246   0.9009
educ          2.3196     7.1087  0.3263   0.7443

# instead of
summary(model)

Call:
lm(formula = wage ~ educ)

Residuals:
     Min       1Q   Median       3Q      Max 
-2058.77  -251.34    -4.47   264.48  2258.63 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)    9.485     69.421   0.137    0.891
educ           2.320      5.545   0.418    0.676

Residual standard error: 515.7 on 998 degrees of freedom
Multiple R-squared:  0.0001753, Adjusted R-squared:  -0.0008265 
F-statistic: 0.175 on 1 and 998 DF,  p-value: 0.6758

Scaling and Transformations

The Four Types

1. Level-level: \(y = b_0 + b_1x\)
2. Level-log: \(y = b_0 + b_1\log(x)\)
3. Log-level: \(\log(y) = b_0 + b_1x\)
4. Log-log: \(\log(y) = b_0 + b_1\log(x)\)

Interpreting Log Specifications

Specification	Change in x	Effect on y
Level-level	+1 unit	+\(b_1\) units
Level-log	+1%	+\(\frac{b_1}{100}\) units
Log-level	+1 unit	+\((100 \times b_1)\%\)
Log-log	+1%	+\(b_1\%\)

Why Use Logs?

1. Normalize skewed distributions
2. Reduce impact of outliers
3. Interpret coefficients as elasticities
4. Transform multiplicative relationships to additive

Example: CEO Salaries

data("ceosal1", package = "wooldridge")
par(mfrow=c(1,2))
plot(salary ~ sales, data = ceosal1, 
     main = "Raw Values")
plot(log(salary) ~ log(sales), data = ceosal1, 
     main = "Log Transformed")

Non-Linear Relationships

• Not all relationships are linear
• Can add polynomial terms: \(y_i = \beta_0 + \beta_1x_i^2 + u_i\)
• Visual inspection is crucial
• Always plot your data first!

Note

Linear in linear regression means linear in parameters not variables

Remaining things for you to sudy

• Read up on the properties of the conditional expectation in Math Refresher B
• Read up:
  • 2-6: Regression through the Origin and Regression on a Constant
  • 2-7: Regression on a Binary Explanatory Variable

next class we will start chapter 3