Panel Data and Fixed Effects

Moshi Alam

Motivation

So far we have dealt with a single cross-sectional dataset
The biggest challenge to causal inference is selection bias because we do not observe the counterfactual
We have learned how IVs can help us solve the endogeneity problem
But IVs are not always easy to find — especially good ones
Often, data over multiple time periods can reveal interesting patterns and provide additional variation to consistently estimate parameters of interest
… especially if the unobservables that make our estimates inconsistent do not change over time

Motivation (continued)

Panel data are additionally important because:

They are required to understand policy impacts
They allow us to study how causal impacts evolve over time
Many policies are staggered in implementation, necessitating panel data
- Will discuss this more details in a couple of classes when we get into Difference-in-Differences
Even when the question of interest is not a policy evaluation, observing the same units over time can be very informative

Types of Data Over Time

Panel data
- Balanced panel: every unit observed in all time periods
- Unbalanced panel: some units missing in certain time periods (attrition)
  - PSID – Panel Study of Income Dynamics
  - NLSY – National Longitudinal Survey of Youth
  - Most administrative datasets (e.g., tax records) are panel
Repeated cross-sections
- Different units observed in each time period
- CPS – Current Population Survey
- NHIS – National Health Interview Survey
Time series

Panel Data & Fixed Effects

Credits: Bunch of materials drawn from Florian Oswald; Nick C. Huntington-Klein

Cross-section vs Panel

Cross-section: one time snapshot per unit \(i\): \(\hat{\beta_{OLS}} = \frac{\sum_i (x_i - \bar x)(y_i - \bar y)}{\sum_i (x_i - \bar x)^2}\)
Panel: multiple time periods \(t\) per unit \(\color{blue}{i}\): \(\hat{\beta_{FE}} = \frac{\sum_{\color{blue}{i}} \sum_{\color{red}{t}} \left(x_{\color{blue}{i}\color{red}{t}} - \bar x_{\color{blue}{i}}\right)\left(y_{\color{blue}{i}\color{red}{t}} - \bar y_{\color{blue}{i}}\right)}{\sum_{\color{blue}{i}} \sum_{\color{red}{t}} \left(x_{\color{blue}{i}\color{red}{t}} - \bar x_{\color{blue}{i}}\right)^2}\)
Panel: index \((i,t)\); track units over time
Benefit: control unobserved time-invariant heterogeneity \(c_i\)
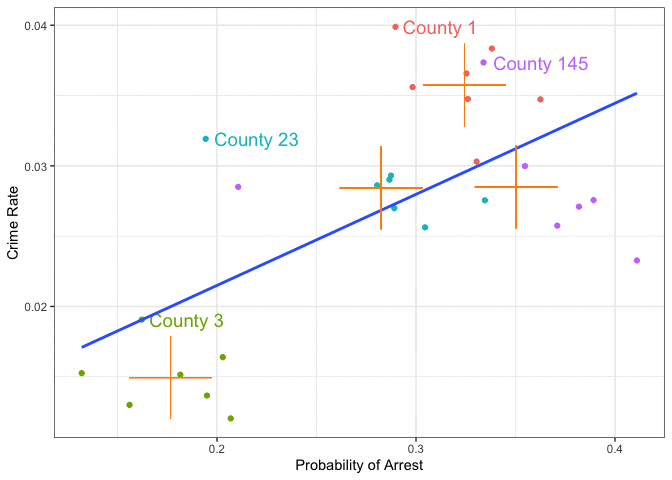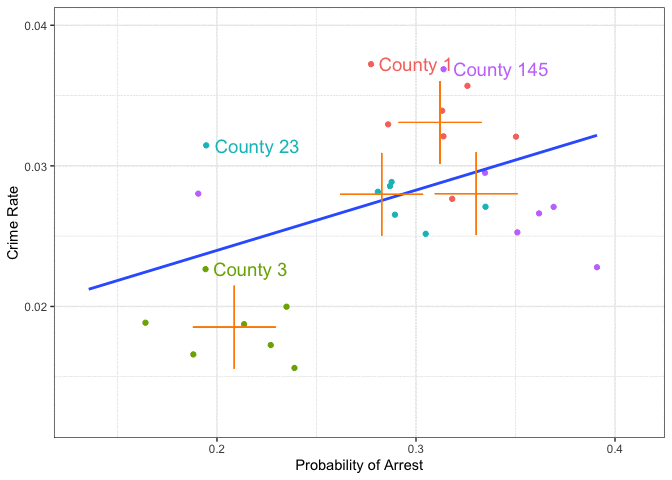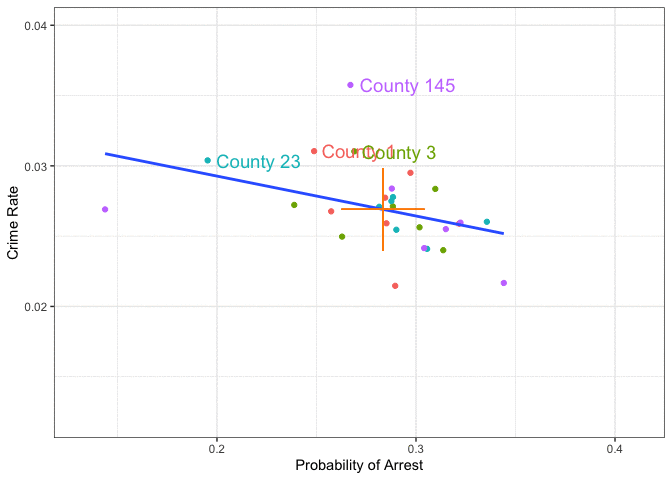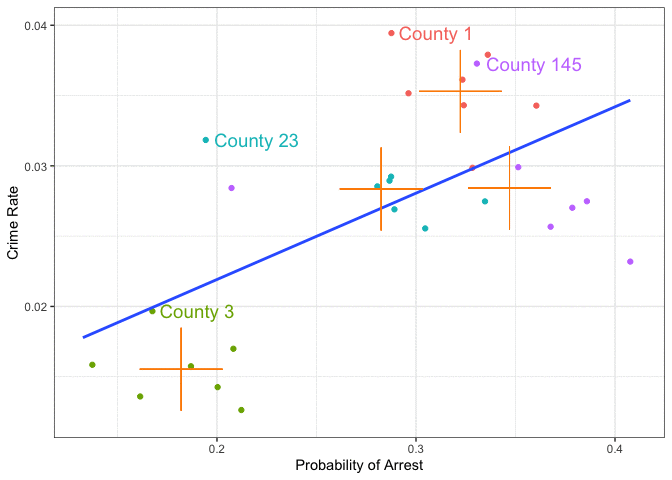
Deterrence question: does higher arrest probability reduce crime?

data(crime4)
crime4 %>% select(county, year, crmrte, prbarr) %>% arrange(county, year) %>% head()

  county year    crmrte   prbarr
1      1   81 0.0398849 0.289696
2      1   82 0.0383449 0.338111
3      1   83 0.0303048 0.330449
4      1   84 0.0347259 0.362525
5      1   85 0.0365730 0.325395
6      1   86 0.0347524 0.326062

Raw pattern

css = crime4 %>% 
  filter(county %in% c(1,3,145, 23))  # subset to 4 counties

ggplot(css,aes(x =  prbarr, y = crmrte)) + 
  geom_point() + 
  theme_bw() +
  labs(x = 'Probability of Arrest', y = 'Crime Rate')

Pooled OLS

summary(lm(crmrte ~ prbarr, data = css))$coef["prbarr",]

    Estimate   Std. Error      t value     Pr(>|t|) 
0.0648010359 0.0159005783 4.0753886238 0.0003839695

css = crime4 %>% 
  filter(county %in% c(1,3,145, 23))  # subset to 4 counties

ggplot(css,aes(x =  prbarr, y = crmrte)) + 
  geom_point() + 
  geom_smooth(method="lm",se=FALSE) + 
  theme_bw() +
  labs(x = 'Probability of Arrest', y = 'Crime Rate')

Naive Interpreting the Cross-Section

Literally: counties with a higher probability of arrest also have a higher crime rate.
Does this imply that more crime leads to more efficient policing?
Or that higher police presence deters crime — but only once it gets bad enough?
What determines police efficiency?
- Could depend on poverty, local laws, political commitment, or other local factors.
🤯 There are clearly many omitted factors in this simple model — we cannot tell whether the estimated relationship makes sense causally.

What Varies Between and Within Counties

LocalStuff — fixed county characteristics (e.g., geography, institutions).
LawAndOrder and CivilRights — political and institutional traits that may change slowly, but are mostly fixed over short horizons.
Police budgets and Poverty levels — vary within counties over time, reflecting local and macroeconomic fluctuations (national)
Can panel data allows us to separate time-invariant county traits from time-varying factors — helping us get closer to a causal interpretation?

Within county patterns

css = crime4 %>% 
  filter(county %in% c(1,3,145, 23))  # subset to 4 counties

ggplot(css, aes(x = prbarr, y = crmrte, color = factor(county))) + 
    geom_point() + 
    #geom_smooth(method = "lm", se = FALSE) + 
    theme_bw() +
    labs(x = 'Probability of Arrest', y = 'Crime Rate', color = 'County')

Within county patterns

css = crime4 %>% 
  filter(county %in% c(1,3,145, 23))  # subset to 4 counties

ggplot(css, aes(x = prbarr, y = crmrte, color = factor(county))) + 
    geom_point() + 
    geom_smooth(method = "lm", se = FALSE) + 
    theme_bw() +
    labs(x = 'Probability of Arrest', y = 'Crime Rate', color = 'County')

Within county means

Panel Model with Unit FE

\[ y_{it} = \beta x_{it} + \underbrace{c_i + u_{it}}_{\text{error}} \] - \(c_i\) may correlate with \(x_{it}\) → OLS biased \(E(c_i + u_{it} \mid x_{it}) \neq 0\) - Simple OLS mixes within + between; biased if \(Cov(x_{it}, c_i) \neq 0\). - Between: differences across \(i\) (time-invariant) → drives pooled OLS bias
- Within: changes over \(t\) within \(i\) → identifies \(\beta\) under FE assumptions

css <- crime4 %>% filter(county %in% c(1,3,23,145))
m_cs <- lm(crmrte ~ prbarr, data = css)
coef(m_cs)["prbarr"]

    prbarr 
0.06480104

FE approach: control for \(c_i\) by allowing unit-specific intercepts or FIXED EFFECTS

FE Assumptions (succinct)

\[ y_{it} = \beta x_{it} + \underbrace{c_i + u_{it}}_{\text{error}} \]

Strict exogeneity: \(E[u_{it} \mid x_{i1},…,x_{iT},c_i] = 0\)
No perfect collinearity: time-invariant regressors drop in FE
Errors: correlation within \(i\) → cluster by \(i\)

Three Estimators (same \(\hat\beta\))

LSDV (dummies): \[ y_{it} = \beta x_{it} + \sum_{i=1}^{N-1} \gamma_i 1\{i\} + u_{it} \]
First-difference (FD), \(T=2\): \[ \Delta y_i = \beta \Delta x_i + \Delta u_i \]
Within (demeaning), \(T\ge2\): \[ y_{it} - \bar y_i = \beta (x_{it} - \bar x_i) + (u_{it} - \bar u_i) \]

LSDV (Dummy-Variable OLS)

m_lsdv <- lm(crmrte ~ prbarr + factor(county), data = css)
summary(m_lsdv)


Call:
lm(formula = crmrte ~ prbarr + factor(county), data = css)

Residuals:
       Min         1Q     Median         3Q        Max 
-0.0052637 -0.0014554  0.0000986  0.0009928  0.0083848 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)        0.044945   0.004556   9.866 9.85e-10 ***
prbarr            -0.028376   0.013629  -2.082  0.04865 *  
factor(county)3   -0.024996   0.002544  -9.824 1.07e-09 ***
factor(county)23  -0.008498   0.001658  -5.126 3.41e-05 ***
factor(county)145 -0.006500   0.001596  -4.072  0.00047 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.002912 on 23 degrees of freedom
Multiple R-squared:  0.8926,    Adjusted R-squared:  0.8739 
F-statistic: 47.78 on 4 and 23 DF,  p-value: 8.115e-11

Adds intercept for every county → recovers within county slope.

library(modelsummary)
cdata <- css %>%
  group_by(county) %>%
  mutate(mean_crime = mean(crmrte),
         mean_prob = mean(prbarr)) %>%
  mutate(demeaned_crime = crmrte - mean_crime,
         demeaned_prob = prbarr - mean_prob)
mod = list()
mod$dummy <- lm(crmrte ~ prbarr + factor(county), css)  # i is the unit ID
mod$xsect <- lm(crmrte ~ prbarr, data = cdata)
mod$demeaned <- lm(demeaned_crime ~ demeaned_prob, data = cdata)
gom = 'DF|Deviance|AIC|BIC|p.value|se_type|R2 Adj. |statistic|Log.Lik.|Num.Obs.'  # stuff to omit from table
modelsummary::modelsummary(mod[c("xsect","dummy","demeaned")],
                           statistic = 'std.error',
                           title = "Comparing (biased) cross-setcional OLS, dummy variable and manual demeaning panel regressions",
                           coef_omit = "factor",
                           gof_omit = gom)

Comparing (biased) cross-setcional OLS, dummy variable and manual demeaning panel regressions
	xsect	dummy	demeaned
(Intercept)	0.009	0.045	0.000
	(0.005)	(0.005)	(0.001)
prbarr	0.065	-0.028
	(0.016)	(0.014)
demeaned_prob			-0.028
			(0.013)
R2	0.390	0.893	0.159
R2 Adj.	0.366	0.874	0.126
F	16.609	47.777	4.900
RMSE	0.01	0.00	0.00

Manual Within Transformation

cdata <- css %>%
  mutate(y = crmrte, x = prbarr) %>%
  group_by(county) %>%
  mutate(y_dm = y - mean(y), x_dm = x - mean(x)) %>%
  ungroup()

m_within_manual <- lm(y_dm ~ x_dm, data = cdata)
summary(m_within_manual)


Call:
lm(formula = y_dm ~ x_dm, data = cdata)

Residuals:
       Min         1Q     Median         3Q        Max 
-0.0052637 -0.0014554  0.0000986  0.0009928  0.0083848 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)  
(Intercept)  1.190e-18  5.175e-04   0.000   1.0000  
x_dm        -2.838e-02  1.282e-02  -2.214   0.0358 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.002739 on 26 degrees of freedom
Multiple R-squared:  0.1586,    Adjusted R-squared:  0.1262 
F-statistic:   4.9 on 1 and 26 DF,  p-value: 0.03583

Same slope as LSDV
Intercept is 0 by construction.

First-Differencing

dt <- as.data.table(css)[order(county, year)]
dt[, y := crmrte]; dt[, x := prbarr]
dt[, `:=`(dy = y - shift(y), dx = x - shift(x)), by = county]
m_fd <- lm(dy ~ dx, data = dt[!is.na(dy)])
summary(m_fd)


Call:
lm(formula = dy ~ dx, data = dt[!is.na(dy)])

Residuals:
       Min         1Q     Median         3Q        Max 
-0.0089587 -0.0015629 -0.0002049  0.0019199  0.0103419 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.0002985  0.0008554  -0.349    0.730
dx          -0.0096765  0.0196879  -0.491    0.628

Residual standard error: 0.00413 on 22 degrees of freedom
Multiple R-squared:  0.01086,   Adjusted R-squared:  -0.0341 
F-statistic: 0.2416 on 1 and 22 DF,  p-value: 0.6279

With \(T=2\), FD \(\equiv\) FE.
For \(T>2\), FE typically more efficient if errors are not well-behaved in differences.
Let’s use a package which can worry for us about efficiency and clustering fixest.

`fixest::feols` (recommended)

m_fe_1w <- feols(crmrte ~ prbarr | county, data = css, cluster = ~ county)

modelsummary::modelsummary(
  list("Pooled (lm)" = m_cs,
       "LSDV (lm)" = m_lsdv,
       "Within (manual lm)" = m_within_manual,
       "FE (fixest)" = m_fe_1w)
)

	Pooled (lm)	LSDV (lm)	Within (manual lm)	FE (fixest)
(Intercept)	0.009	0.045	0.000
	(0.005)	(0.005)	(0.001)
prbarr	0.065	-0.028		-0.028
	(0.016)	(0.014)		(0.005)
factor(county)3		-0.025
		(0.003)
factor(county)23		-0.008
		(0.002)
factor(county)145		-0.007
		(0.002)
x_dm			-0.028
			(0.013)
Num.Obs.	28	28	28	28
R2	0.390	0.893	0.159	0.893
R2 Adj.	0.366	0.874	0.126	0.874
R2 Within				0.159
R2 Within Adj.				0.122
AIC	-198.4	-241.0	-247.0	-243.0
BIC	-194.4	-233.0	-243.0	-236.4
Log.Lik.	102.197	126.516	126.516
F	16.609	47.777	4.900
RMSE	0.01	0.00	0.00	0.00
Std.Errors				by: county
FE: county				X

Syntax: y ~ x | FE1 + FE2 + ...
Cluster by the unit for valid SEs with serial correlation.

Interpretation (within effect)

\(\hat\beta_{\text{FE}}\): effect of a within-county change in \(prbarr\) on \(crmrte\), holding time-invariant county traits fixed.
A change \(\Delta prbarr = 0.10\) implies \(\Delta crmrte \approx 0.10 \times \hat\beta_{\text{FE}}\) (within a county over time).

So we started from here with POLS

Pooled OLS: Mixing Within and Between Variation

FE: Within Transformation

multiple time periods \(t\) per unit \(\color{blue}{i}\): \(\hat{\beta_{FE}} = \frac{\sum_{\color{blue}{i}} \sum_{\color{red}{t}} \left(x_{\color{blue}{i}\color{red}{t}} - \bar x_{\color{blue}{i}}\right)\left(y_{\color{blue}{i}\color{red}{t}} - \bar y_{\color{blue}{i}}\right)}{\sum_{\color{blue}{i}} \sum_{\color{red}{t}} \left(x_{\color{blue}{i}\color{red}{t}} - \bar x_{\color{blue}{i}}\right)^2}\)

The within transformation centers the data!
By time-demeaning \(y\) and \(x\), we project out the fixed factors related to county
Only within county variation is left.
Made by Nick C Huntington-Klein. 🙏

Time-Invariant Regressors

Variables constant within \(i\) (e.g., geography) are absorbed and not identified in FE.
- Absorbed by \(c_i\).
For example if you have tax panel data of individuals over time and you add an individual fixed effect, what are examples of variables that you cannot estimate the effect of?
Options (if you need to udnerstand the efffect of some variable):
- interact with time

Two-Way Fixed Effects

Motivation

Often, we want to control for common shocks that affect all units in a given time period
- e.g., national business cycles, federal policy changes, macroeconomic shocks
We can add time fixed effects \(\tau_t\) to control for these common shocks
This leads to the Two-Way Fixed Effects (TWFE) model
- \[ y_{it} = \beta x_{it} + c_i + \tau_t + u_{it} \]
- Unit fixed effects \(c_i\) control for time-invariant heterogeneity across units \(i\)
- Time fixed effects \(\tau_t\) control for common shocks to all units across time periods \(t\)

Two-Way Fixed Effects (TWFE)

Add common shocks \(\tau_t\): \[ y_{it} = \beta x_{it} + c_i + \tau_t + u_{it} \]

m_twoway <- feols(crmrte ~ prbarr | county + year, data = crime4, cluster = ~ county)
etable(m_fe_1w, m_twoway, se = "cluster")

                          m_fe_1w         m_twoway
Dependent Var.:            crmrte           crmrte
                                                  
prbarr          -0.0284* (0.0052) -0.0011 (0.0026)
Fixed-Effects:  ----------------- ----------------
county                        Yes              Yes
year                           No              Yes
_______________ _________________ ________________
S.E.: Clustered        by: county       by: county
Observations                   28              630
R2                        0.89258          0.87735
Within R2                 0.15859          0.00034
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interprets \(\beta\) net of unit and time effects.
IN the next two weeks, we will see how this is a foundational model for policy evaluation

Comparing POLS, FE, TWFE

m_pooled <- lm(crmrte ~ prbarr, data = crime4)
m_fe   <- feols(crmrte ~ prbarr | county, data = crime4)
m_twfe <- feols(crmrte ~ prbarr | county + year, data = crime4, cluster = ~ county)

modelsummary::modelsummary(list(
  "Pooled"   = m_pooled,
  "FE"     = m_fe,
  "TWFE (fixest)"   = m_twfe
))

	Pooled	FE	TWFE (fixest)
(Intercept)	0.043
	(0.001)
prbarr	-0.038	-0.002	-0.001
	(0.004)	(0.003)	(0.003)
Num.Obs.	630	630	630
R2	0.129	0.871	0.877
R2 Adj.	0.127	0.849	0.855
R2 Within		0.001	0.000
R2 Within Adj.		-0.001	-0.002
AIC	-3347.3	-4373.6	-4394.6
BIC	-3334.0	-3969.1	-3963.4
Log.Lik.	1676.651
F	92.646
RMSE	0.02	0.01	0.01
Std.Errors		by: county	by: county
FE: county		X	X
FE: year			X

References & Credits

Some slides/materials adapted from Florian Oswald, Nick C. Huntington-Klein (Nick Klein)

Panel Data and Fixed Effects

Motivation

Motivation (continued)

Types of Data Over Time

Panel Data & Fixed Effects

Cross-section vs Panel

Raw pattern

Pooled OLS

Naive Interpreting the Cross-Section

What Varies Between and Within Counties

Within county patterns

Within county patterns

Within county means

Panel Model with Unit FE

FE Assumptions (succinct)

Three Estimators (same \(\hat\beta\))

LSDV (Dummy-Variable OLS)

Manual Within Transformation

First-Differencing

fixest::feols (recommended)

Interpretation (within effect)

So we started from here with POLS

FE: Within Transformation

Time-Invariant Regressors

Two-Way Fixed Effects

Motivation

Two-Way Fixed Effects (TWFE)

Comparing POLS, FE, TWFE

References & Credits

`fixest::feols` (recommended)